

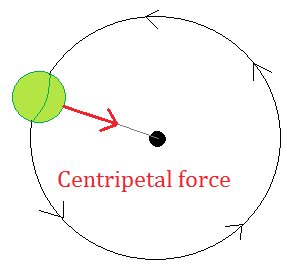
Because r is given, we can use the second expression in the equation ac v2 r ac r2 to calculate the centripetal acceleration. If the rope makes an angle of 30º with the horizontal during circular motion, calculate the angular velocity of the weight. By converting this to radians per second, we obtain the angular velocity. If the space station has a diameter of 550 m, calculate the rotational speed needed to simulate 1g of gravitational acceleration.Ī 15 kg weight is attached to a rope and spun in uniform circular motion with a 0.5 m radius as shown. The diagram shows a futuristic space station designed to simulate gravity in a weightless environment. What is the magnitude of the centripetal force required to maintain the motion of the ball? Practice Question 2Ī particle is moving around in a circle of radius 1.5 m with a constant speed of 2 ms -1. The maximum centripetal acceleration we have is a 3.8 meters/second squared, and the maximum speed at which these slot cars can run without flying off the track is: V 1. When are both constant, the centripetal force is directly proportional to the. The angular velocity of the motion is `4pi rad s^-1`. Find the angular speed of Earth around the Sun in radians per second. Centripetal force M 2 R or in terms of velocity v Centripetal force M v2/R Centrifugal force is the reaction force and acts radial outwards. If point P has a mass M, then the force required to accelerate this mass radial inwards is found from Newtons 2nd Law. Example 3: Find the distance from the Earth to the Sun if you know that the Orbital speed of the Earth is 29,800 m/s and, of course, that it makes one revolution around the Sun in 1 year. In another formula, if the given radius r is larger, F would be greater.
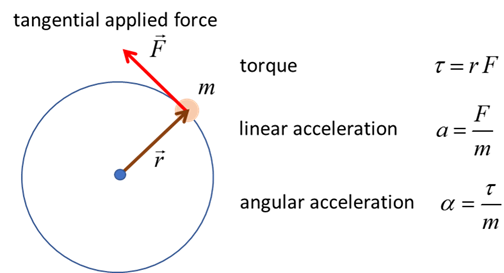
Using the tool above in linear speed calculator mode will confirm the math. In one formula given below, if the given radius r is larger, F would be lesser. The plane of the circular path is horizontal. the change in velocity and so centripetal acceleration is radial and inwards. We simply use the formula rad r / v 20 / 0.5 0.0250 radians per second. The curved motion is maintained so long as this net force provides the centripetal force requisite to the motion.Practice Question 1 (NESA Sample Question)Ī 15-gram metal ball bearing on a string is swung around a pole in a circle of radius 0.8 m. The resultant or net force on the ball found by vector addition of the normal force exerted by the road and vertical force due to gravity must equal the centripetal force dictated by the need to travel a circular path.
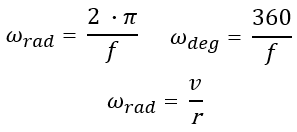
This centripetal force is not a third force applied to the ball, but rather must be provided by the net force on the ball resulting from vector addition of the normal force and the force of gravity. The centripetal force demanded by the curved motion also is shown above. There are two forces one is the force of gravity vertically downward through the center of mass of the ball mg where m is the mass of the ball and g is the gravitational acceleration the second is the upward normal force exerted by the road perpendicular to the road surface man. The centripetal is the force required to hold a body having mass M and distance R from the center of rotation and moving at a tangential velocity V. Acceleration is defined as the rate of change of velocity, and velocity has a direction. If there is a change in the angular velocity w, then. How is this possible Intuitively, if we increase the radius of the circular path, we would need lesser centripetal force to keep it on the path. Apart from any acceleration that might occur in the direction of the path, the lower panel of the image above indicates the forces on the ball. Constant acceleration (change of direction) requires a constant force, which is described by F(mv2)/r if v is measured in ms-1 or Fmomega2r if omega is measured in rads-1. There always is a centripetal acceleration and centripetal force whenever an object is moving in a circle. In one formula given below, if the given radius r is larger, F would be lesser.


 0 kommentar(er)
0 kommentar(er)
